The smallest mad weave (anyam gila) basket

Paul Gailiunas has summarized the math and history of closed triaxial weaving, also known as anyam gila, or mad weaving. I have marked up one of his images below to emphasize the triangle grid that this kind of weaving respects.

Anyam gila weaving with its triangle grid.

Braiding background

In the usual flat braiding of three strands, the strand in the middle is exchanged with the strand on the left, then the strand in the middle is exchanged with the strand on the right, etc. Each strand thus spends only one move in the middle, but spends two consecutive moves on the right side or the left side. The weaving elements in anyam gila enjoy a similar lifestyle. They spend only one triangle inside the thickness of the fabric each time they pass through it (anyam gila is three plies thick,) they spend two triangles facing out each time they visit the front or the back face of the fabric. Overall the period is six triangles long: two in front, one in the middle, two in back, one in the middle.

The smallest anyam gila basket

The smallest anyam gila basket uses a single weaver, six triangles long, to wrap a two-sided triangle three-plies thick on each side. In the figure below, the single weaver has been cut somewhat narrow to clarify the structure.

The smallest anyam gila basket.

There are three kinds of edges, each triangle having one edge of each kind: meadow, tunnel, and scarp. The terms come from fancifully viewing the mad weave fabric as a network of wildlife overpasses and underpasses, as in this figure:

The view from one tunnel to the next: mad weaving as a network of wildlife underpasses and overpasses.

If the fabric is viewed as assembled from triangles, the meadow edge of a triangle always pairs up with the meadow edge of another triangle; scarp edges pair up with tunnel edges and vice-versa: there is a scarp above every tunnel, and a tunnel below every scarp.

Here is how the meadow/meadow fold looks in the basket above, viewed in cross-section.

Cross-sectional view of the meadow/meadow boundary in the simplest anyam gila basket.

And here is the same boundary in a larger basket where it is not folded:

Cross-sectional view of a meadow/meadow boundary in a large basket (not folded.)

At a meadow/meadow boundary nothing seems to happen---nothing changes on either side of the fabric. In the cross-sectional view we can see that a meadow/meadow boundary conceals a discontinuity in the middle stratum of the fabric. Therefore the choice of which diagonal of the quadrilateral is the meadow/meadow edge is not arbitrary, and the quadrilaterals on both faces of the fabric exactly coincide.

Here is how the tunnel/scarp fold looks in the basket above, as viewed in cross-section.

The tunnel/scarp fold in the simplest anyam gila basket. 

And here is the same boundary in a larger basket where it is not folded:

Tunnel/scarp boundary in a larger basket.

In the cross-sectional view we can see that a tunnel/scarp boundary on one side of the fabric coincides with a scarp/tunnel boundary on the other side of the fabric.

Two polarities of triangles

Joining two triangles at their meadow edges forms a quadrilateral with two scarp edges and two tunnel edges. Since the scarp edges coincide with the two parallel edges of a single weaver, the scarp edges must be opposing edges of the quadrilateral (and likewise for the tunnel edges.) Therefore, there are two possible polarities of triangles: ones that are meadow/tunnel/scarp in clockwise order and those that are the same in counterclockwise order. Each quadrilateral in an ayam gila weave is composed of a pair of triangles of the same polarity.

The polarity of the quadrilaterals tells the handedness of the weaving

The fact that there is a meadow/meadow edge dividing each quadrilateral means that there are also two possible polarities of quadrilateral: sighting down the meadow/meadow boundary we may see the scarp on the left or the right. The quadrilaterals in an anyam gila weave are all of the same polarity, including those on the reverse face. (The meadow/meadow boundary is in the same location on either face; going to the other side reverses our orientation, but the tunnel/scarp to scarp/tunnel correspondence compensates for the reversal.) The polarity of any quadrilateral tells the handedness of the weaving.

Building fabrics in traveling salesman (TSP) order

It's real simple. Choose a map of the surface. Choose a subset of map's edges that constitutes a spanning tree. Place the quadrilateral truchet tiles of the previous post so that the dashed line coincides with the map edge if that edge is in the spanning tree; otherwise, orient the tile so that the dashed line coincides with the dual edge. Choose a place to start the knitting, and the tiles do the rest. Every shape: no increases or decreases.

A TSP knitted fabric: narrow knitting with picked up stitches

A traveling salesman (TSP) knitted fabric. The black represents ribbons of knitting. The dotted lines indicate picked up stitches.

A form of knitting that can be represented by the generic quadrilateral truchet tile described in the previous post is "narrow knitting with picked up stitches." In this technique, the thread paths in the generic tile represent ribbons of knitting. Where the thread paths come close together in the center of the tile, the second-pass of knitted ribbon picks up stitches from the selvedge of the first-pass of knitted ribbon.

This technique does not produce a solid fabric, rather a fabric with variously shaped openings at every vertex.

This technique can make any orientable surface. (It can also make any non-orientable surface if the knitting stitch is garter stitch, or any other stitch with identical faces.)

A generic truchet tile for fabric structures

A generic quadrilateral truchet tile for fabric structures. (This tile is "inked-through": flipping the tile over shows its mirror image.)

A closed surface of any complexity can be cut or broken into simple pieces (i.e., topological disks.) Let's look at this in more detail, considering only orientable surfaces---those surfaces where we can consistently distinguish "outside" and "inside."

For example, if we cut a piece from a surface that is simple except for having a hole in its middle, we can make an additional cut from its periphery to the boundary of the hole to eliminate the problem. Another example: if the piece is simple except for having a handle in its middle, cutting all the way across the piece, underneath its handle, converts the piece into a cylinder. A cylinder (topologically speaking) is just a disk with a hole in its middle, so we can make a second cut to eliminate the problem.

Place a vertex everywhere a cut ends, or rejoins itself, or intersects another cut, then we can see our simple pieces as polygons in a broad sense: we allow the sides of a polygon to be nonplanar curves, we allow a polygon to have as few as one sides, and we allow a polygon to have monovalent as well as the usual multivalent vertices on its periphery.

As a simple example, here are cuts that separate a sphere into simple pieces (a 12-sided piece and nine 4-sided pieces.)

Cuts dividing a sphere into a 12-sided piece and nine 4-sided pieces.

So now we have all polygonal pieces. Proceed to chop all the polygons into triangles: create a new vertex in the center of each polygon, and cut the piece like a pie, making cuts from the vertices on the periphery to the new vertex in the center. (Do this procedure even if a polygon happens to be a triangle already.)

Secondary cuts (dashed lines) cutting all ten polygonal pieces into triangles.

Now we have exclusively triangular pieces. We proceed to glue the primary cuts back together again. We do this in a way that records the former location of each primary cut with a solid line. Since each repaired cut joins two triangular pieces, the result is a polygon with 2 * 3 - 2 = 4 sides. Now we have cut the surface exclusively into quadrilaterals. Each repaired cut (marked by a solid line) is a diagonal of a quadrilateral.

Every orientable, closed surface can be cut into quadrilaterals with distinguished diagonals. The distinguished diagonals comprise the edges of a map of the surface, the remaining diagonals comprise the edges of the dual map.

The above is a well known mathematical fact, but it is nonetheless technologically exciting because it means that any technology that can be described by quadrilateral truchet tiles can populate any closed, orientable surface.

We now repair the secondary cuts as well, recording their former location with dashed lines. The surface is now fully reassembled, and looks like the diagram immediately above. We will now use this diagram as the template for placing quadrilateral truchet tiles.

As drawn, the dashed-line triangles composing the 12-sided polygon are very distorted. In that portion of the surface, we will not attempt to distort the truchet tiles correctly; we will simply show them with white gaps between them. It will be evident in the following diagrams how portions of the truchet tiles need to be distorted to mate up across the gaps.

The quadrilateral truchet tile we are going to place (first image above) represents a generic fabric structure. It can represent crochet, net tying, linking, looping, peyote stitch, balloon tying, unit weaving and others. (Among those it cannot represent are knitting and nalebinding.) The procedure described here is for making a surface from a single thread, working along an advancing front of finished fabric, the work ending exactly where it started.

The generic truchet tile is an "inked through" tile: flipping it over reveals its mirror image. In each quadrilateral opening there are eight ways this tile can be played. The choices are: whether or not to flip the tile over, and, then, which of four possible orientations to choose in placing it.

Because working order is a concern, we must begin with a simple operation that fixes a working order. To do this: find primary cut that is part of a cycle of primary cuts and gray it out; repeat the previous step until no black-edged cycles remain. The black edges remaining are a spanning tree. Here is a spanning tree for the example.

A spanning tree (black edges.)

Placement rules:

Rule 1: Threads must not cross black edges; they must cross gray edges. 

Rule 2: The first pass of the thread through the tile follows the route and direction indicated by the drop's point. (The indicated direction is into the concavity of the drop.)

Tiling procedure:

0. Arbitrarily choose some edge as the origin. 

1. Place a tile on the origin edge in an orientation satisfying Rule One. 

2. Guided by the drop's point, find the next edge. (If the next edge is already occupied by a tile, continue along the indicated route of the thread until you come to an unoccupied next edge, or until the fabric is complete.) 

3. Place a tile on the next edge in an orientation satisfying Rule One. 

4. Flip the tile (i.e., rotate it 180 degrees around either of its diagonals, or both) until the established route and direction comports with that indicated by the tile per Rule Two.

5. Go to step 2.

The first few tile placements in this example:

First tile.

Second tile.

Third tile.

Fourth tile.

Fifth tile.

Sixth tile.

Seventh tile.

Eighth tile.

Ninth tile.

Completed fabric.

Fabric techniques (continued)

Many fabric techniques can be represented by a pair of generic quadrilateral truchet tiles. The single yarn that makes the fabric passes through each tile twice. Each time it passes through, it enters and exits through adjacent edges of the quadrilateral. Each edge of the quadrilateral plays a unique role as either the entrance, or the exit of either the first, or the second pass.

A nice property of orientable surfaces is that these two sequential passes are always countercurrent (even in high genus surfaces.) That, together with the fact that we need to color the first and second passes differently, means we need two generic truchet tiles that are mirror images of each other.

In the pair of generic truchet tiles shown here, the first pass is shown bright white, the later pass is colored faded gray.

In almost every technique, not much happens on the first pass: a loop of yarn is simply left behind for the second pass to seize upon. An asymmetrical teardrop shape is used in these two tiles to indicate a generic fabric technique that accomplishes most of its work on the second pass.

Most fabric techniques can make every orientable surface

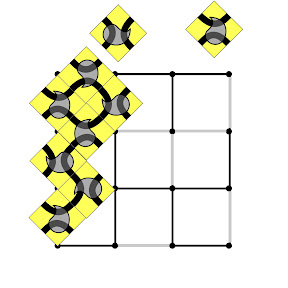
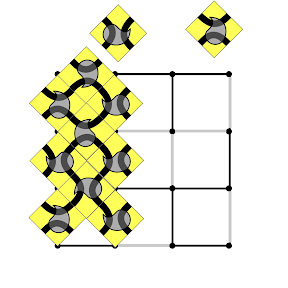
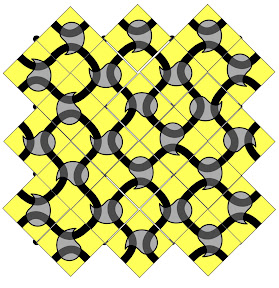
The world offers many examples of closed surfaces, some of them rather daunting to the basket maker. Beyond weaving, there are several other fabric techniques that can make baskets: knitting, crochet, linking, looping, net tying, macrame, balloon tying, etc. So the question arises, "What fabric techniques can make which closed surfaces?"

The heartening answer is that most fabric techniques can make every orientable closed surface. This answer holds true even if we restrict ourselves to working with a single length of yarn that is spliced to itself, end-to-beginning, at the conclusion of the work.

Math Preliminaries

A graph is a set of vertices, some pairs of of which are connected by edges. In a general graph (the only kind of graph that concerns us here) an edge is allowed to connect a vertex to itself, and as well, an edge is allowed to connect the same two vertices as some other edge.

General graphs are usually represented diagrammatically with vertices drawn as dots on a surface, joined by edges drawn on the surface as curved lines. Whenever we draw a graph in this way, we are imposing a cyclic ordering of edges around each vertex, an ordering that is not intrinsic to the abstract graph. A graph, together with a surface, and a cyclic ordering of edges at the vertices that allows it to be drawn on the surface without edges crossing is called an embedding. 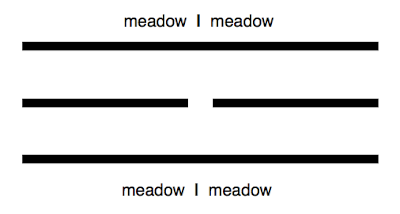An embedding is called proper if deleting the points under the drawing would cause the surface to fall apart into a topological disk or disks.

Not topological disks.

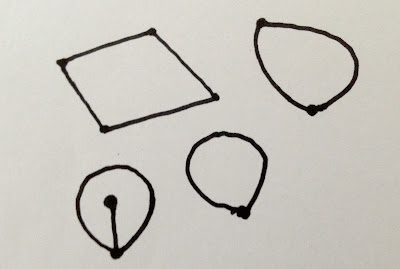Topological disks.

What's a topological disk? For example, a disk containing a handle, or an interior hole, or an interior slit, is not a topological disk; but a sphere with a hole, or a slit, or a disk having a slit in its periphery, is a topological disk.

Neither graphs nor surfaces are necessarily connected, but, by a sensible convention, a "properly embedded graph" always means a one-component graph properly embedded in a one-component surface.

A surface is orientable if it is possible to make a consistent choice of surface normal vector at every point. Non-orientable surfaces, such as a Klein bottle, can only be tiled with truchet tiles if flipping tiles over makes no difference—most truchet tiles for fabric structures are not like that, so we are mostly limited to making orientable surfaces. That is a big disappointment mathematically, but perhaps of little practical importance (there's a good reason why nothing ever comes packaged in a Klein bottle.)

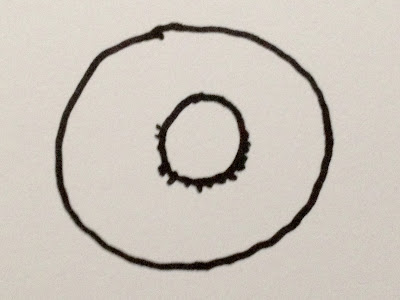An orientable surface.

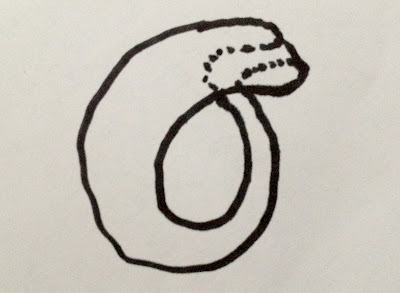A non-orientable surface—a Klein bottle.

Duality

Every properly embedded graph (call it the primal) has a properly embedded dual. The dual has the same number of edges as the primal, but they have been, so to speak, rotated by about 90 degrees, so that they connect at the center of faces they once went around, and go around vertices where they once connected. In effect the role of the edges is maintained, while the roles of vertices and faces are exchanged. As implied by the name, this relationship is reciprocal: the primal is the dual's dual.

Superposition of any primal with its dual implicitly cuts the surface into quadrilaterals. (Visualize the two positions of  each edge as the two diagonals of a quadrilateral.) This is a well known mathematical fact, but its enormous practical significance is under-appreciated: every surface (or, at least, every orientable surface) is a playground in every possible way for any technology that can be described by a quadrilateral truchet tile. As we will see, there are a lot of technologies that want to play at this game.

Quadrilateral Truchet Tiles

Quadrilaterals are not generally squares, of course, but our truchet tiles need to be stretchy enough to accomodate the shape of any quadrilateral. With that understanding, there is no harm in idealizing both the quadrilateral truchet tiles and the surface quadrilaterals they will be placed on as being squares.

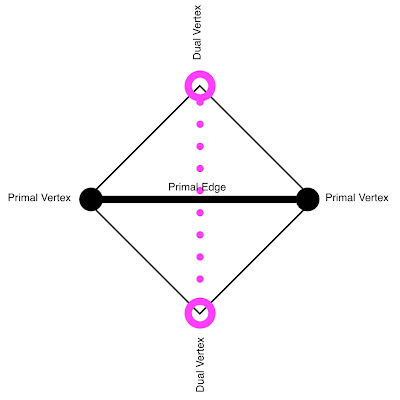A surface quadrilateral idealized as a square.

As shown above, each of the surface quads has a primal diagonal terminated by primal vertices, and a dual diagonal terminated by dual vertices. The primal edge corresponds to one of the original graph (i.e., one of the cuts that divided the surface into topological disks.)

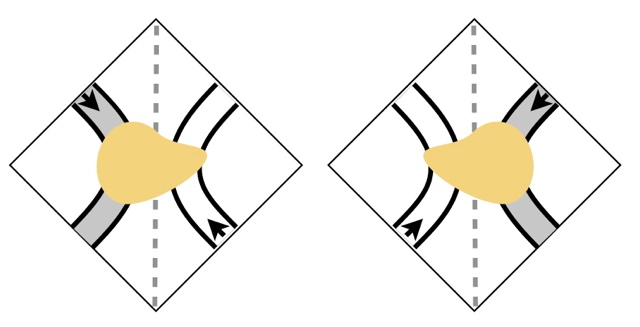
We will assume an oriented surface, so there is never any confusion in playing our truchet tiles "right side up." That still leaves four possible ways to rotate a quadrilateral tile when placing it on the surface. Of course, if a particular truchet tile has 4-fold rotational symmetry, there is no real choice, all four orientations are equivalent.

In the other cases, if the truchet tile has a designated primal diagonal, we may find that this primal diagonal has been played parallel or perpendicular (loosely speaking) to the primal edge of the surface quadrilateral. If the truchet tile has 2-fold rotational symmetry, there's no need to inquire further: a 180 rotation will make no difference.

In the other cases, if the primal diagonal of the truchet tile has been oriented, and likewise the primal or dual edge in the surface quad (whichever lies under the tile's primal diagonal) must have an orientation, so that we can speak of the tile being placed in a co or anti orientation to the underlying surface quadrilateral.

Working Order

In weaving we generally do not care how many threads (weavers) will be used, or in which direction they are to be laid in, but in most other fabric-making techniques it is desirable to work with a single thread, one that is consistently oriented from start to finish. That implies playing our game with truchet tiles having oriented primal diagonals, and placing them in a sequence that corresponds to the start to finish passage of the single thread.

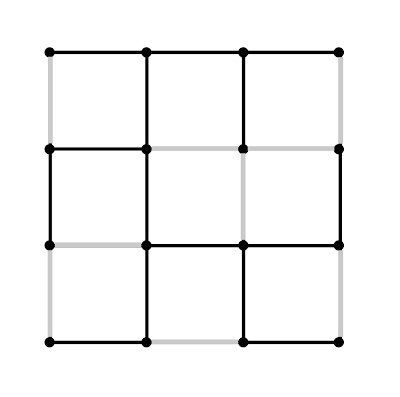
A reliable way to find a route over the surface for the single thread is to find a subset of the graph of primal edges that forms a spanning tree, that is, a connected, acyclic graph containing all of the primal vertices. Finding a spanning tree in a graph is an easy task. One algorithm is to add some new vertex to the empty tree and try to add every incident edge, excepting only those that connect to a vertex already in the tree (as that would constitute a cycle.) Repeat for all the newly added vertices...etc. When no more edges can be added, the spanning tree is complete. Another algorithm, one easier to do by eye, is to begin with the complete graph, erase any edge that is part of a cycle, repeat until no cycles are left.

A spanning tree effectively colors every surface quadrilateral as tree or non-tree.

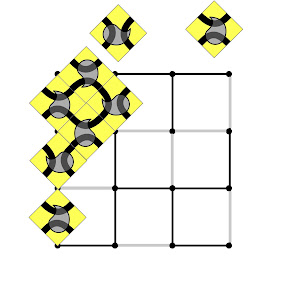
Running the thread in a way that does not cross edges in the spanning tree, but always crosses edges that are not in the spanning tree, yields a serpentine loop of thread that visits the entire surface.

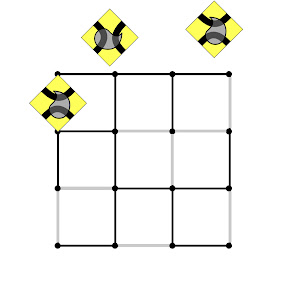
In the following the primal diagonal of each truchet tile is chosen so that a proper placement of a tile is parallel in the tree quadrilaterals and perpendicular in non-tree quadrilaterals.

(To be continued.)

Universality of peyote stitch (and linking, and looping, and knotted looping)

Peyote stitch

Linking 

Looping 

Knotted Looping

The map operation medial converts any map into a map that is 4-regular and chess-colorable. Once chess-colored, all the faces in a particular color, say black, are connected via their corners. Therefore, a map defined by placing a vertex in the middle of every black-colored face, with connecting edges iff the two faces touch at the corners, is connected. (Note that this 'new' map is either the original map or its dual, depending on the color choice.) Since this new map is connected, it has at least one spanning tree. If we circumnavigate this spanning tree while staying on the edges of the chess-colored map, the result is an Euler non-crossing circuit in the chess-colored map. This circuit is a possible working order to realize the surface in peyote stitch (or linking, or looping, or knotted looping.)

Every spanning tree in the primal map (or its dual) directs an Euler non-crossing circuit in the medial; each of these, in turn, directs a Hamilton circuit in the truncate of the medial (a.k.a., the bevel of the primal map, which is the same map as the bevel of the dual.)

Medial map (chess-colored)

Dual map

Triangular truchet tile for linking.

Triangular truchet tiles for looping.

If the surface is genus zero, the peyote stitch working order is represented by an undip word, since the beads (or links, or loops, or knots) are simply photon edges.

Primal map

Thus, multiple ways to weave, link, loop, or knot a given surface are directly derivable by map operations from any of its maps.

Beating Plowshares into Traveling Salesmen

Fabric making traditionally advances in a plowing (boustrophedonic) order, or a spiral order when worked in the round. These two working orders suffice, topologically speaking, to make any closed surface (after all, a closed surface is just a plane polygon with sewn-up edges,) but practically speaking these patterns are very restricting when we need to accommodate different densities of detail. (By the time a closed surface has been stretched out into a polygon there are always varying densities of detail.)

The solutions to the Traveling Salesman Problem are versatile in accommodating such variations in density, as proven by the image above, quoted from the Egg-Bot Wiki.

But, working in TSP order means we must be able to turn both left and right while working on the same side of the fabric...