Penrose tiling corrugations

The Penrose tiling of rhombs, a non-periodic tiling of the plane, can be approximated by corrugated (i.e., diagonally folded) squares. Projected onto the plane, such an approximation cannot be exact because diagonally folded squares do not project as rhombs unless the diagonal fold is parallel to the plane, and, when that is the case, all such rhombs project their longer diagonal at true length. The rhombs in the Penrose tilings have longer diagonals of two different lengths, so they cannot be projections of diagonally folded squares of the same size.

This taped-together paper model (shown from each side in the two images) mimics the arrangement of rhombs in a small portion of a Penrose tiling. Though the imitation of the Penrose tiling is approximate, the assemblage manages to remain reasonably flat.

There are two ways to weave this corrugation pattern from straight strips: the straight strips can be composed of whole squares or they can be composed of diagonally-cut half squares. The latter is the way a quad-faced map is normally converted to plain weaving: it adds a weave opening at the center of each square in addition to those at the corner of each square.

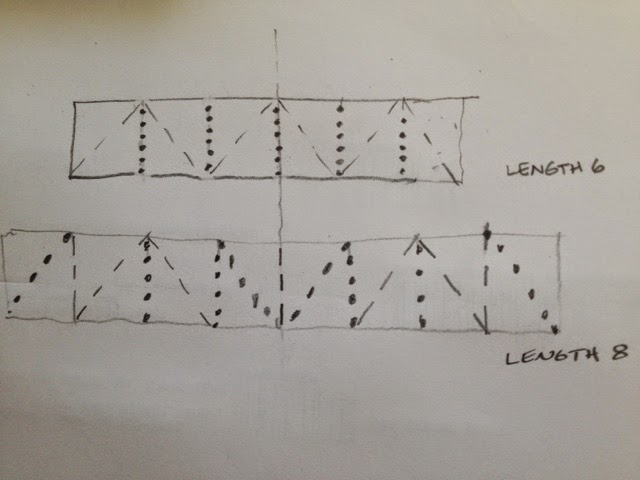
When the straight weavers are composed of squares, there are only two kinds of weaver in this passage, both have cosine-like symmetry in their folding.

In each square within a weaver there are four possibilities, either of the two diagonals of the square can be chosen for the fold and, the fold can be mountain (dotted) or valley (dashed).

Ten of each kind of weaver is needed to weave this passage.

Voxel weaving versus corrugated kagome

A woven cube (a single woven voxel).

Voxel weaving and corrugated kagome are similar weave patterns. Both are made with straight weavers having 90-degree folds, in both techniques the exposed portions of each weaver are squares. Corrugated kagome always produces a corrugated surface; voxel weaving sometimes produces a corrugated surface—the exceptions are when the basket surface is parallel to the x, y, or z plane. Voxel weaving rigidly maintains angular orientation over the whole basket (i.e., each square is perpendicular to either the x, y, or z axis); corrugated kagome permits folding along the diagonal of the square (whether or not this fold is part of the corrugation pattern) so every angular orientation is possible.

A corrugated kagome unit-weaving of an octahedron. The exposed portion of each weaver is a square with a diagonal fold.

A diagonal fold in corrugated kagome corresponds to an edge in the underlying triangulation. Therefore, in flat passages with zero corrugation frequency there are not any diagonal folds. In such a passage corrugated kagome and voxel weaving are indistinguishable.

In a flat passage, zero-frequency corrugated kagome and voxel weaving are indistinguishable. The triangles are the underlying triangulation of the corrugated kagome weaving.

Since is not possible for the triangulation of a closed shape to be entirely flat, there is always some place in a zero-frequency corrugated kagome weaving where diagonal folds appear. Therefore, there is no example a closed basket that is both voxel-woven and corrugated kagome.

Where to go from here? Since a flat passage cannot a basket make, there is no way to make a basket that is both voxel-woven and corrugated kagome.

Weaving voxellated surfaces

A surface is weavable if it has a chess-colorable tessellation. The tiles of the tessellation represent the openings in the weaving, and their colors indicate the handedness (left or right) of the helix made by the weavers that go around the opening. (The weavers themselves are represented by the color boundaries between the tiles.) From that information, it is easy to deduce whether a weaver goes over or under—no matter which face of the fabric we happen to be looking at.

For example, a chessboard, as shown above, represents a simple tabby weave. A handy thing about the tabby weave is that we can pick a width for the weavers that precisely covers the surface leaving only tiny weave openings.

We can tabby-weave a cube as is shown by the coloring of the "rounded" cube in the figure above (note that the external edges of the cube, shown rounded off, are not color boundaries and thus do not represent weavers.) The pattern of the weavers forming this cube are like the three loops of string one might use to tie a parcel. The chess-coloring of the surface proves that these three loops can be put in consistent over-and-under weaving order.

Imagine that every voxel in a quantized space is like the tabby-weave cube shown above, differing in having been translated in x, y, and z to its proper position and rotated so that its corner colors match its neighbors' at that corner. Notice that every solid body formed by a union of such tabby-weave voxels is wrapped by a chess-colored tessellation. Therefore, the surface of every voxellated object can be woven in tabby weave.

Weaver length and the closure problem

Work in Progress III by Dasa Severova.

Traditional baskets are generally left open, but structural baskets generally need to form a closed shape. Closure involves splicing, but it is a different kind of splicing than used to extend a weaving element while the fabric is being worked: a closing splice work into fabric that is already largely complete. That involves feeding a weaving element through multiple crossings, a difficult task that is made even harder if the basket surface is corrugated.

A chain is no stronger than its weakest link, and a basket is no stronger than its closing splice. Seeking high basket strength by weaving long elements gets us nowhere if the closure cannot be made with weavers of the same length.

Insisting on putting a splice everywhere a splice can be placed (in order to avoid the teleological problem) leads to very short weavers, but long weavers that would be too long to complete a closing splice offer only illusory strength.

Interlocking pucks at the non-three-way engagements

Design for a single-impression corrugating tool for frequency-11, length-2 pucks. When the faint pink squares are 9 cm on a side the scale is appropriate to the aluminum sheets that can be cut from soda cans.

Length-2 polyphase unit-woven corrugated kagome weavers (pucks) can be locked together as they are assembled if the corner points are bent to engage circular bays cut in the profile where the non-three-way engagements would otherwise be.

The teleological problem in polyphase unit weaving

Though it seems desirable to use longer unit weavers in the interest of fabric strength, a difficulty arises: the entire work must be predesigned in order to know the correct placement (orientation and phase) of new crossing pieces as they are encountered in the work. (Recall that the entire basket could be a an alternating knot, in that case the orientation and phase of every unit would have been fixed by the first crossing.)

To avoid this troublesome rigidity in the weaving process it is necessary to use non-directional unit weavers ( "S"- and "Z"-shaped, not "W"-shaped) and non-directional layering (i.e., brick-laid, not shingled.)

Also, there must be a splice everywhere it is possible to have a splice, otherwise the question of how to phase the next crossing weaver would arise.

Due to these condiderations, the only possible not-teleological unit weavers are "Z"- and "S"-units two triangles in length. Placing "Z"-units on one face and "S"-units on the other, covers all the splices on both faces.

Weaving bricks

A puck weaver of length 2 and corrugation frequency 3.

There is a "teleological" problem in polyphase unit weaving when the composite, polyphase weavers are shingled. Shingling effectively assigns to each composite weaver an orientation, i.e., the direction that the units "lean."As new crossing weavers are encountered in building up the basket surface, the entire basket would need to have been designed in advance in order to know which orientation to start them in.

Brick-laid unit weavers do not have an orientation, and thus escape this difficulty. Since all weavers form closed loops of even length, identical puck "bricks" that form these loops by being laid end-to-end  must have even length. In fact for the greatest versatility of shape they must have length two.

That leaves very little overlap for bricks in adjacent courses to engage one another, so higher frequency corrugation is useful for greater stiffness and frictional engagement between courses. The little puck "brick" pictured above begins to gain some inevitability.

In a single-layer course of these bricks laid end-to-end, spliced squares alternate with un-spliced squares. The un-spliced squares are the ones that the over-and-under pattern of kagome weaving will expose on that face. On the other face, the spliced squares of this course will be covered by the un-spliced squares of the other course.