Saturday, October 20, 2012
Print bumper stickers for 25 cents and 1 minute each
Wednesday, October 10, 2012
Thursday, October 4, 2012
How to evolve a balloon animal
Evolve a unique genetic code by playing a word game, then learn to twist the balloon animal that your genetic code describes! Over 200 kids at World Maker Faire NY 2012 participated in this hands-on activity that introduces the concepts of genotype/phenotype mapping and mutation.
- paper and pencil
- a #160 balloon (#160 balloons are nominally 1" diameter and 60" long when inflated)
- a small-diameter pump suitable for inflating #160 balloons
Sources: Qualatex makes reliable #160 twisting balloons and a suitable pump (the #47512 pocket pump.) You can find them sold online.

First Rule:
You can insert ud or np anywhere.

Definition: according to the direction of their strokes, there are two kinds of letters: the up letters, u and d; and the down letters, n and p.
Second Rule:
An up letter can shuffle past a down letter.
Now, make a clean copy of your word at the stage in its evolution when it is just four letters long. That's an ample length for your first attempt at balloon twisting.
Now you're ready to twist.
At the last letter there is a special rule: stretch the nozzle of the balloon (the place where you started) and wrap it around the twist where you finished. Ta da!
You started with an abstract word in a four letter alphabet (the genotype) and have twisted the observable entity it specifies (the phenotype.) Each edit in the derivation of the word can be seen as a mutation.
Can these particular mutations ever produce a word with an odd number of letters? A word that ends with an open letter?
Can more than one word specify (map to) the same phenotype?
Why do we allow only one mutation per generation? (Is it ever likely that two closely interacting mutations would originate in a single individual?)
If we splice or insert one of these genotypes into another genotype, is the result still a word we can twist?
For longer words, you will need to stop after completing the last letter the current balloon can accommodate. Then stretch and wrap the nozzle of the next balloon around the last twist, and keep going!
Thursday, September 27, 2012
Maker Faire



Friday, August 17, 2012
Evolve Your Own Balloon Animal
A mathematical paper on ballon twisting turned me on to this sculptural technique. Shapes that can be unit-woven using undip words can also be twisted from balloons if we represent "photon" edges by lengths of balloon doubled back on themselves. This selective doubling of one-third of the edges turns a three-valent (weavable) structure into a four-valent (balloon-twistable) structure.
To absorb a photon we now simply thread the "electron" path through it and push the twisted portions together. Twisted balloons easily hold this sort of rudimentary join in place.
The method for evolving the undip words is of course the same as for "Evolve Your Own Basket," presented at the USA Science and Engineering Festival this spring. The two rules in the word game are:
- Rule 1. You can insert ud or np anywhere.
- Rule 2. An up letter (u or d) can be shuffled past a down letter (n or p).
I am hoping to present this activity at World Maker Faire New York at the New York Hall of Science, September 29 and 30, 2012.
Sunday, April 29, 2012
Evolve a Basket at USA Science and Engineering Festival
Tuesday, March 20, 2012
Reminiscences on skybows

In the late 90's, Tony Frame and I developed a rotating ribbon arch kite that we called a skybow. I provided most of the engineering ideas, but none of it would have happened without Tony's driving encouragement and his part in the flight testing and design iterations. I wrote at the time that flying a skybow was like playing with "an anti-gravity rope" because, held across the wind between two fliers, a spinning skybow "sags" up the way an ordinary rope sags down. In favorable winds, a skybow can form a tall, leaning, horseshoe-shaped arch, typically many tens of meters in length. A skybow is a soft kite in the sense that there are no struts, and it coils up compactly after flying. The controversy over whether a skybow really is a kite at all is probably ongoing, the arguments being summarized early on in an article on skybows by Steve McKerrow and Valerie Govig in the Winter 1997-8 issue of Kite Lines magazine.
The outstanding characteristic of a skybow is its rather absurd length-to-width ratio. Mr. Big, with a 16mm chord (flown on the Washington Monument grounds in the fall of 1997) was 300m long (as measured lying on the ground)—in that dimension it was probably one of the largest kites ever flown—at the same time, in the chord dimension, it was probably one of the smallest kites ever flown. We later flew a 17mm-chord skybow that was just over 400m long (one quarter of a mile) on the Washington Monument grounds during the 2002 Smithsonian Kite Festival. My petite girlfriend (now my wife) started shrieking so much at seeming to be pulled straight up into the air (though I doubt the tension was really much more than 30 pounds) that Tony, ever discrete, took himself to another part of the field. A skybow does not really have all that high a lift-over-drag ratio—magnus-effect airfoils are not very good at L/D in any case, and the effective aspect-ratio is reduced by the twisting of the ribbon—but when a skybow is misaligned to the wind, the downwind side of the arch can seem very steep. Hence the skybow flyers' rule: "up moves up, down moves down." (For example, if your side of the arch seems to be lying down, you need to move downwind.)
The 400m record in 2002 was an easy attempt. Four-and-a-half years after Mr. Big, we were flying a skybow twice as strong to only one-third greater length. Attempting another record had been simply a matter of dedicating that much hardware to the task and having a place to fly. The 400m skybow, consisting of seventeen 24-meter sections, (an amalgam of the sections and hardware we had left over) was put together for Kites with Lights (which is held each year the weekend after Thanksgiving in Nag's Head, North Carolina) the preceding fall. I had found that lightsticks could be spliced into the middle of skybow sections (the length of the lightstick aligned to spin and carry tension.) Burdened with lightsticks in this way, a skybow still flies smoothly in a good wind. Since this flight was going to be at night, I felt free to use all our left over hardware, whether it matched or not. I drove down to North Carolina that day without (typical of me) having finished all the lightstick splicing. I recall finishing the splices with time running out at a campground picnic table, much to the fascination of a small flock of peahens who shared the otherwise empty campground with me. It was incredibly warm that late November evening, shirtsleeve weather. I had been too ambitious in thinking I could deal with 400m of skybow in the dark by myself. After several false starts, and tangles in bushes, I managed to keep nine sections flying—looking like a new constellation in the night sky. I came to the opinion then that seven or nine is the right number of lights on an arch. Fewer, and you struggle to see the arch, more, and it becomes like a Christmas lighting contest with no place to stop. Later that night, I flopped down on the same picnic table and looked up at the stars. After hours of eye practice connecting nine stars in an arch, the real constellations looked like a bowl of spaghetti.
During the same late-nineties era, Roy Mueller of Wind Mueller Aerology Lab in Boca Raton, Florida, independently developed a rotating arch kite that is stabilized by a different principle. We were corresponding and sharing samples at the time. It is fair to say that Tony and I were jealous of the Mueller design's ability to form tall arches with short lengths, and Roy may have envied our design's performance in high winds. Roy's design, which had a cross-section that popped into classic airfoil shape when uncoiled, seemed more affected by aerodynamic pressure (or centrifugal force) in high winds. But that was years ago. I see that the Wind Mueller Lab is still coming out with new commercial skybow designs, ones that I am not familiar with.
In contrast, our skybow design was a dynamically stabilized flat ribbon. It did not seem to care how fast the wind was blowing, or how fast it was spinning, as long as the arch was shortened enough to keep the tension in the ribbon in a safe range. I had the pleasure and excitement of flying a 80m-long skybow in sustained 50 mph winds at Jockey Ridge State Park in Nag's Head, North Carolina. The noise was incredibly loud—like a Harrier jet landing on your head—and that was in a situation where the wind itself was so loud you needed to yell to be heard 20m.

That magnificent sand park at Nag's Head is like a square mile of the Sahara lost in North Carolina. In its swales it is easy to find yourself alone with sand and sky. My favorite memory of skybow flying, apart from the Woz-and-Jobs camaraderie with Tony, was flying there on a perfect morning. I think it was the morning after their annual kite festival, when everyone had cleared out. When you stake one end of a long skybow you forget about that end, you are just holding on to this shimmering, roaring filament that comes down to you from the void. That morning the concentration of the flying experience was almost transcendental, it brought out for me how much the experience of kite flying is about the mysterious upward-pulling string, not about what is at its end.
Anyone who has played with a Native-American toy called a bull-roarer will not be surprised that an autorotating airfoil can be an efficient generator of sound. The skybow noise comes up rather suddenly. At 12 mph, it is a hum that is nothing much to notice; at 25 mph it sounds like there must be a NASCAR track somewhere over the next hill; at 50 mph it's an incredible roar right down on top of you. I believe the noise gets louder when the phase-velocity of rotation along the twisted ribbon (an apparent velocity that I call the barber-pole velocity) exceeds the speed of sound in air (345 m/sec.) In that situation, sound generation is evidently both efficient and highly directional.The sound heard is different at different places on flying field, but it is particularly loud for the two flyers at the ends of the arch. The sound is very responsive to tension changes produced by tugging on the handles, which is a fun way to play with a strong wind.
A taut ribbon will not spin stably by itself. That's a fact that will be overly obvious to trained engineers—I say overly, because a skybow proves that under the right conditions a taut, lightweight, unsupported ribbon can spin so smoothly it seems like a laser beam. As a trained engineer, the effectiveness of aerodynamic damping was something I needed to be confronted with in person.
A taut ribbon will not spin stably by itself—it will typically either turn wide-side to the wind, and not spin at all, or go through wild oscillations of spin and translation. But if twisted up enough, it will indeed spin stably. A demonstrator of this is what Tony and I called a wind-womp. Terminate both ends of a 24 yard section of 3/8" corrugated plastic ribbon with 4 feet of light kite string. Hold the resulting assembly across the wind while twisting up the string at one end with a cordless drill (no swivels being used at either end.) As the increasing twist is shared with the ribbon, you will see its behavior in the wind gradually improve. Ultimately, with a lot of twist in the ribbon, it reaches a point where it spins smoothly, and then reverses, alternately flying up and then down, and making a "whomp" sound each time it changes direction.
That is fun, but unfortunately this kind of twist stabilization cannot be maintained when swivels are added to each end to allow a continuous rotation in the "up" direction. We first tried a practical approximation to twist stabilization. Our first skybow was 2" wide, made out of "poly" packing tape. It had built-in discrete twists of 90° about every 10 chord-lengths (as I recall). Each 90° twist was accomplished by fabricating a hollow, elongated tetrahedron out of the same tape. (You could also think of the tetrahedra as universal joints rather than 90° twists, I am not sure which idea was foremost in my mind.) The results flying a 50m length of this sort of skybow on the Washington Monument grounds and the beach at Mason's Neck State Park in Virginia where encouraging, but it was a lot of work to make kites this way.
In the beginning, it was Tony's idea that we collaborate on a kite. Tony, about ten years younger than me, was the administrator at my church. We had gotten to know and like each other while working on church festivals and mailings with others, and just the two of us developing the church's dial-up electronic bulletin board system (something that came through about a minute before AOL got everyone on the web.) I had been kicking around an idea for an arch of conventional rotor elements and proposed we should try something along those lines. After some small scale experiments in my backyard with chains of polystyrene foam rotors, and then with 1/2" computer magnetic tape (salvaged many years ago when a neighbor threw out some reels of NASA data on the curb,) I came up with a relatively short length of the 2" packing tape with tetrahedra. That was the first flight test we flew together.
My first approaches and results were not all that great. I am pretty sure I would have dropped the whole idea sooner or later if we had not been in this as a team.
I don't remember how I came to the idea that we could stabilize the ribbon dynamically by "mistuning" the twist-wave and translation-wave velocities. The key proved to be adding slack material (deadweight) near the center of the chord. The addition of this mid-chord inertia lowers the translation-wave velocity, but has little effect on the twist-wave because mass added at the mid-chord does not increase the airfoil's moment of inertia. (It is important that the added weight not carry tension, or the weighting effect will be partially or even completely cancelled.)
People always ask how I came up with the idea. The easy (and partly true) answer is that it came one step (and one flight test) at a time. But looking back, I realize that I had deep relevant experience. I started in college on a Civil Engineering track, but fate would have it that I would be in a sophomore Aerospace and Mechanical Sciences class on energy issues in the fall of 1973 when the war broke out that would precipitate the first energy crisis. In response to an open ended assignment, I proposed to my professor, Robert Socolow, the idea of cooling by selective radiation to the night sky exploiting the wavelength band (the so-called atmospheric window) that H2O and CO2 leave open. At the time, I did not know that a research group in Italy was already onto this idea. Prof. Socolow took the initiative to set me up with Noel Amherd to research this idea as independent study in the spring term. By then I was hot to switch to Aerospace and Mechanical Sciences (they seemed to have all the interesting problems,) but luckily I was still in a Civil Engineering class in transportation studies (because they had all the cool computers.) By that luck, my first experience in computer programming was in APL on an interactive graphics terminal (in those days that was a storage CRT). Some terms later, when I finally took a "real" programming course from the Computer Science department, the state of the art for the undergraduates was still Fortran on punched cards—and then queue up for fan-folded line printer output. That spring (1974,) I spent huge amounts of time in the APL terminal room. I was working on my radiative cooling simulations, and spending no time doing my transportation studies assignments. That experience got me into mechanical engineering, which at Princeton was tightly linked to aerospace engineering, and it also got me started in doing independent study. A senior thesis was not required for engineers, but, Prof. David Haarje, my engineering design professor, suggested that I show an idea I had for a flexible, Magnus-effect wind energy converter to Prof. Thomas Sweeney (well-known for his invention of an aeroelastic airfoil called the sailwing.) Prof. Sweeney and his colleague Barry Nixon very kindly gave me a hearing, but politely suggested I try something closer a little closer to practice. Prof. Sweeney steered me toward doing something with an aeroelastic wind energy converter that I could test, at model scale, in the university's subsonic wind tunnel. The oscillating wind energy converter that I studied for my senior thesis did not have much to do with skybows, but by the summer after graduation my interest had morphed into doing a lot of experiments with stretched tapes in the wind (using, for the first time, that half-inch computer tape rescued from the curb.) At graduate school that fall, I would play hookey from grad student duties, crossing over the Panther Hollow Bridge to do notebook calculations on oscillating ribbons at the outdoor tables in front of the Carnegie Institute in Pittsburgh. All this stuff was buried deep in my head somewhere when Tony and I started talking about kites.
Our most successful skybows were razor-trimmed assemblies of commercial tapes. We added stabilizing weight to our skybows by including a stretchy, thick, narrow tape at the center. Trying to build a symmetrical sandwich of commercial tapes proved problematical as there was always enough stress at the center to cause unsightly local delaminations. Instead, we settled on an unsymmetrical three-layer design, strong on one side, weak on the other—the stress on the adhesive bond being limited by the weaker layer. The main mechanical strength came from a layer of high performance, clear, polypropylene strapping tape from 3M (#863 tape trimmed in the last assembly step to 17mm chord-width), the weighting came from a thick, stretchy, clear polyethylene weathersealing tape (Frost King Weatherseal Tape, trimmed before assembly to 10mm width), and the color came from a thin layer of colored polyethylene film (2-mil Bear Claw bags from Bland Co., trimmed in the same final cut with the polypropylene strapping tape.) The stretchy weighting tape was assembled with its unsticky side against the sticky side of the polypropylene strapping tape. That allowed the thin colored polyethylene film to be in contact with pressure-sensitive adhesive over its full width. The stretchy tape came off the roll with so much tension that a motorized capstan was needed to lower the pre-stress before assembly. Making skybows quickly becomes a matter of making tape-converting machines that make skybows. My homebrew tape-converters never worked very reliably, or without fussing over every few meters, and making unnecessary splices. That, and the cost of converting materials that were themselves at retail prices, was our big problem in trying to go into commercial production. That and the fact no customer anywhere had flown anything like it. A well-tested skybow went to persons who said they were going to fly it at Burning Man. It came back covered with beautiful pink playa dust and complaints that it had not flown.
The center-weighting tape in a skybow is not entirely un-structural. When a taut ribbon is twisted, compression stress builds up across the width. The thickness of the weighting tape in the middle part of the chord helps reinforce the ribbon against buckling in compression.
A skybow can work with swivels just at the two ends. We called this a single-section skybow. We flew single-section skybows that were as long as 114 meters with some success. There is a launching problem with a single-section skybow since the entire length must be supported off the ground to start the ribbon spinning—ultimately, there is a length where this is no longer possible. There is also a performance problem with a single-section skybow since the middle of the arch sees better wind, and lies at a better angle to it, so it wants to spin faster than the two ends. This problem can be avoided by tapering a single-section skybow to a narrower chord near each end—but that only makes the next problem worse. A long, single-section skybow can carry a lot of torque towards one end, where, if anything stops the ribbon from spinning, it will cause a buckling failure of the tape that basically turns the ribbon into twine—for good. For these reasons, as well as the ability to reef in the length of the skybow to suit the wind speed, we settled on making independently-swiveled sections of 20 to 24 meters in length. These could be easily launched or reefed, one section a time, and were nearly immune to the twist-up buckling failure. Swiveled sections of moderate length are also easier to handle on the ground.
When flying a multi-section skybow, it is possible to end up with one section spinning in the wrong (downward) direction. Then there is nothing to be done short of bringing down the entire skybow to that section and relaunching it. To avoid this problem we would "train" the skybow sections to prefer spinning in a particular direction by strongly folding the outboard, unreinforced, portions of the chord in a Z-pattern. The polypropylene tape would almost completely "forget" this creasing, but remember it just enough to strongly prefer spinning in the trained direction. A trained skybow has, in effect, a left side and a right side (as seen looking downwind) that must be respected in setting the skybow up on the flying field.
Under high tension a skybow will sometimes snap. Surprisingly, it is not rare for a skybow to snap in two places at once—some sort of shockwave phenomenon I guess. If that happens, the broken middle portion of the skybow may drift a long ways downwind—something to consider when choosing a flying field.
If repairing (i.e., splicing) a skybow is necessary, anything you do with pressure-sensitive tape will prove temporary. We came up with an expedient we called squiggles. Two sections to be spliced are folded over double and overlapped. The squiggle, a zig-zag, bent piece of piano wire is woven over-and-under (the action is really more like wrapping) the doubled and overlapped ribbon to generate enough friction to hold the splice together permanently.
At the point where each section joins to a swivel, we also used a squiggle fitting. For this fitting, piano wire is bent into a zig-zag portion culminating in an open triangle. The skybow ribbon is made narrower at the end by Z-folding it (in the same direction it was trained) to make it only as wide as the central weighting tape (i.e., about 10 mm.) It is then passed through the triangle (which attaches to the swivel) and doubled over itself. The doubled section is then woven (more accurately, wound) over-and-under through the zig-zag portion. When squiggle fittings are made with enough zig-zags they never slip or fail.
Skybows are hard to see and frustratingly hard to photograph. Dark blue sky and bright white clouds make very different backgrounds for seeing, so no one color is ideal for skybows. Having a color-striped skybow gives at least a chance that one of the colors will be more visible. Since the 3m strapping tape #863 we were using is clear, we had the option of using color-striped polyethylene on one side to color both sides of the skybow. I made color-striped polyethylene tapes by heat-sealing 2-mil polyethylene from "Bear Claw" bags of various colors made by Bland Co. into a wide belt about 1m wide and 4m in circumference (limited by the 2m+ ceiling height in my shop.) Slitting that belt in a helical path gave a long, narrow, polyethylene tape with repeating colored stripes. Most of the striped skybows I made had a pattern that repeated about every 4 meters.
If you fly skybows you will soon learn this truth: twisted is tantamount to tangled. To handle a long length of ribbon without tangling, it must be kept untwisted. If a length of skybow on the ground is being twisted up by the wind, it must be allowed to align downwind, and fast.
Winding spools having cranks can store ribbon without twisting it, but they are dangerous. They can break your fingers with the crank, or friction-burn right through your clothing with the rim. Notice that the usual way of winding onto a crank-less spool puts twist in the unwound portion of the ribbon—which is only permissible if the twist is being freely released to an off-spool swivel.
If you buy cut ribbon in a fabric shop from an experienced clerk she will deftly wrap it (untwisted) in a figure eight on two fingers of one hand. The same approach works to wrap a 24m section of skybow on the forearm. Once slipped off the arm, the untwisted ribbon can easily pay out from the inside of the figure-eight. Cinching these figure-eight hanks with velcro cable ties (which can obligingly stick to one's socks when not in use) became my favorite way to deal with skybows on the ground.
Another way to handle long lengths of ribbon, useful at times, is to stuff the ribbon into a sack (or, indoors, into a pile on the floor) taking care to remove twist as it goes in. It may not seem likely that a chaotic pile of ribbon will remain untangled in a sack, but it will, if you remove all twist before it goes in, and never allow the tag end of the ribbon to enter the sack. This storage method is strictly last-in-first-out.
Five-hundred pound fish don't spin very fast. The relevance of that saying is this. It is easiest to start with homebrew skybows by exploiting ready-made fishing swivels from the tackle shops (only the highest-quality, e.g., SAMPO, ball-bearing swivels will work at all.) The ratings on these swivels are for breaking under tension, not spinning under tension. You need to choose a ball-bearing fishing swivel rated about twenty times the tension you expect in your skybow. Even then, if you keep the swivels out of the dirt, the life will only be a few outings.
We ended up making our own swivels using miniature sealed ball bearings of the type used in model racing cars. The seals add some friction, but are essential for long life. Because they have high-volume uses, these ball bearings are relatively inexpensive. They are not ideal however. The ideal bearing for a skybow would be specified for its high thrust forces and low radial forces, it would twist the ribbon less than standard bearings. We used a MR115-2RS ball bearings from Boca Bearings in a housing cold-forged out of a thin-walled brass tube and a shaft cold-forged out of thick-walled brass tube. This lightweight design survived occasional operation at 50 lbs tension.
We had limited success trying to scale up skybows to a wider chord. Springbows are a stretchy sort of skybow made by weaving a ribbon through a helical polyester spring of triangular section. A springbow won a kitemaker's award at the 2004 Smithsonian Kite Festival in Washington DC (just as the skybow had in 1999.) A springbow can be just a few meters long and about 7 cm chord, but it will not handle a wide range of wind speeds.
It is often a challenge to scale up a kite because everything wants to scale up geometrically, which in turn causes weight per unit area (and thus required wind speed) to scale up as well. We can hope to get around this by exploiting better materials and smarter designs to prevent weight per unit area from scaling up in proportion to the chord dimension. The situation with rotor kites is unfortunately more hopeless. An auto-rotator must have a certain inertia in proportion to the cylinder of air that surrounds it in order to autorotate smoothly. Thus we are forced to scale weight per unit area up in proportion to the chord dimension—no matter how good our materials or designs. Bigger rotors need higher wind speeds. Too bad.
But we can hope to make skybows longer. Length is just a matter of the specific strength of the ribbon and the ability of the swivels to handle the tension. I have no doubt that a 1 kilometer skybow is already possible using a high-performance composite ribbon. One mile (1.6 km) may be too far from where we are now.
Actually, better performance might be had from the same materials by taking some of the fat out of the design. Here is the weight budget for a 4 gm/m skybow with a 17 mm chord:
Mass Budget of Old Skybow Design:
PP tape (film only) 1.1 g/m
PP tape (adhesive only) 0.5 g/m
PE colored film .8 g/m
PE centerweighting film (11 mm wide, including weight of adhesive)1.6 g/m
-----------------------------------
4 g/m
The PP tape adhesive and the colored film are not necessary; a little less mass could be dedicated to the centerweighting if it was more concentrated in the center, giving a leaner design.
Mass Budget of Lean Skybow Design
PP film 2.8 gm/m
centerweighting 1.2 gm/m
----------------------------------
4 g/m
The lean design has 2.5 x as much structural material (the PP) at the same weight. Since the first type of skybow has flown at 400m length, the leaner design (which will pull 2.5 x as hard) should be able to fly at 1000m length. What is needed is swivels that can handle 2.5x the tension.
Monday, March 19, 2012
Deformations: 21 genetic variants of udud
This is a recently completed sculpture, Deformations, that I hope to show this July at Bridges 2012 at Towson University in Baltimore, Maryland. It contains the 21 different versions of the digonal prism that can be made from flexeez by playing the individual flexeez either long or short.
Multiple undip words describe the digonal prism. Here are all eight synonyms for the digonal prism in u-n-d-p alphabetical order:
uudd
unpd
udud
udnp
nudp
nnpp
npud
npnp
They all make the same shape, but if you use a consistent coloring convention (I use pink/purple/green, pink = 1st energy color, green = photon color) some will come out colored differently. I tend to remember udud as the undip word for the digonal prism (rather than any of the seven other equally good synonyms,) so that is how I wove these colorings. The choice of word and coloring is really arbitrary, but it helps to be consistent.
Playing the individual flexeez either "long" or "short" produces what a chemist would call a deformation isomer, a chemical structure that differs only in bond length. Each open letter represents a Y-join where two flexeez are added to the work, each closed letter represents a Y-join where one flexeez is added to the work. To annotate the deformation isomers, I markup the undip word, adding two accents to open letters, and one accent to closed letters. Keeping that rule completely consistent, the extra accent that is needed at the first letter (which is always open) is added to the last letter (which is always closed, and where no other accent is ever needed.) I begin weaving by reading the accent at the very end of the word.
Overall, there are exactly one-and-a-half accents (and flexeez) per letter and, of course, there are an even number of letters, 2n, in the undip word. If the shape we are making is unsymmetrical, then all of the different ways of playing the flexeez long or short make geometrically different shapes. Therefore, there will be 2^(3n) different deformation isomers of an unsymmetrical shape. If the shape has some topological symmetry (as the digonal prism does) some of the different markups will describe the same shape. For example, the digonal prism has only 21 deformation isomers, though it has 2^(3*2) = 64 different markups.
Using a prime to indicate a flexeez played long, and a star to indicate a flexeez played short, and always considering the flexeez added at each Y-join in right-to-left, counter-clockwise order (a convention that comes naturally in twog weaving, but is rather arbitrary in weaving flexeez,) here are the 21 markups I wove for Deformations:
1. u''d'u''d'
2. u*'d'u''d'
3. u**d'u''d'
4. u**d*u''d'
5. u**d'u*'d'
6. u''d*u''d'
7. u'*d*u''d'
8. u*'d'u*'d'
9. u*'d'u'*d'
10. u''d*u''d*
11. u'*d*u'*d'
12. u'*d*u*'d'
13. u*'d*u''d*
14. u**d*u**d*
15. u'*d*u**d*
16. u''d*u**d*
17. u**d'u**d*
18. u*'d'u**d*
19. u'*d*u'*d*
20. u'*d*u*'d*
21. u**d'u**d'
Sunday, March 11, 2012
The simplest flexeez toruses
Here is the trivalent theta graph:
Wednesday, March 7, 2012
Weaving binary distortion isomers from accented undip words
Represent a flexeez played "long" by a prime ('), and one played "short" with a star (*). A convention that comes naturally to twog weaving (but is hardly necessary in weaving flexeez) is to consistently take the units added at a given vertex in a counterclockwise, right-to-left order. Notice that at a vertex described by an open letter, two units are added to the work; at a vertex described by a closed letter, one unit is added to the work. After each letter in the undip word, append primes and stars, one for each unit added at that vertex, taken in the counterclockwise, right-to-left order. The first and last letters are anomalous: the first letter adds three units to the work, the last letter adds none. A convenient solution is to append the extra prime or star (needed at the first letter) onto the last letter (where none is needed.) Then we gain the hard and fast rule that open letters have two accents, closed letters have one. (The weaver must look ahead at the accent on the last letter in order to orient the very first piece in the weaving.)
The color convention in the weaving shown in the following photographs is that pink is the first energy color, purple is the second; green is for photons.
Here we are weaving:
u'*n'*d'p*
A big help in weaving distortion isomers is observing the convention that long plays are played right-side-up, and short plays are played upside-down. With the flexeez brought in in the right order and flipped in the right way, rather less thinking is involved in getting it properly into the work.
Here is the work after the first letter, u'*:
Notice that we read ahead to the asterisk on the last letter, p*, to learn that the first flexeez is played short. Here is the work after the second letter, n'* :
After the third, d' :
After the fourth and final letter, p* :
And the completed binary distortion isomer, u'*n'*d'p* :
The following eight accented undip words suffice for all eight distortion isomers of the tetrahedron:
u''n''d'p'
u*'n''d'p'
u*'n''d*p'
u**n''d'p'
u**n*'d'p'
u**n'*d'p'
u**n''d*p'
u**n''d'p*
Binary distortion isomers of baskets
In chemistry, a distortion isomer is a chemical compound distinguished from another chemical compound solely by a difference in the length of one or more of its chemical bonds. The incredibly versatile Flexeez construction toy makes it practical to explore this topic as it relates to baskets and surface meshes.
Flexeez go together a zillion different ways, but only one will concern us here: three flexeez can be joined to form a rigid Y-shaped connection around an inner triangle that supplies the rigidity:
It is natural to form such a Y with long arms, but each of the three flexeez in the Y can be be independently flipped over and rotated 90° to become a short arm. This of course alters the shape of the inner triangle as well—thereby changing the relative angles of the arms—but topologically nothing changes:
It proves possible in practice to assemble any genus zero (sphere-like) basket with any or all of its flexeez flipped over from "long" to "short."
I call flexeez baskets that differ only in the way their flexeez are played (long or short) binary distortion isomers of each other. Binary because there are just two options for bond length when weaving with flexeez. Note that whether a given edge has been played "long" or "short" is a matter of perspective. For example, a basket in which all flexeez have been played short, could also be seen as the dual basket in which every flexeez has been played long. If some particular isomer is distinguished as the primal isomer the confusion is eliminated.
A fully unsymmetrical, or chiral, basket with n edges (i.e., using n flexeez) has 2^n distortion isomers (counting the original.) By that count, the tetrahedral basket, having 6 edges, would have 2^6 = 64 binary distortion isomers. But symmetry reduces the number of distortion isomers having distinct shapes. Being highly symmetrical, the tetrahedral basket has binary distortion isomers in only 8 (not 64) different shapes, as shown in the photo above.
Here are the four binary distortion isomers of the theta graph on the sphere:
Here are the six binary distortion isomers of the monogonal prism:
Thursday, February 23, 2012
Visualizing map operations as vertex inflations
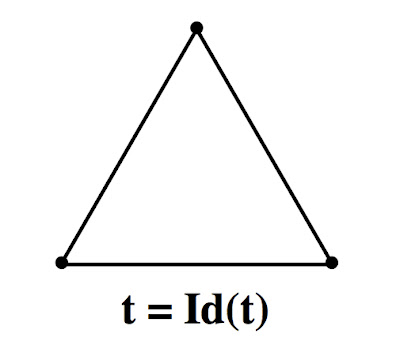
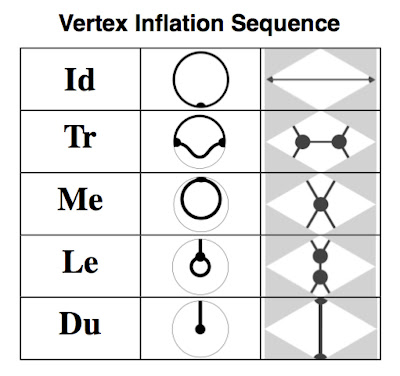
We have drawn the triangle on the sphere, though it may look like we have drawn it on the plane. Given any topological map on the sphere, we can place all but perhaps one vertex on the front side of the sphere. We will draw spherical maps on the plane in this way, knowing that occasionally we will need to imagine what is happening at a singular point on the back side of the sphere.
OK, let’s dispense with drawing little black dots at the vertices, except where they are 2-valent and needed, and redraw the original vertices as little bubbles. This already gives us the truncate of the base map.
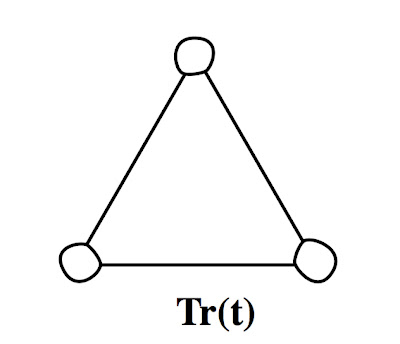
Inflate the vertices some more, and eventually they meet each other at the midpoint of the edges. That forms medial:
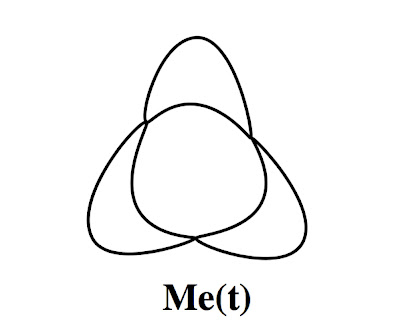
Continued inflation of the bubbles causes the frontier of meeting to enlarge from a point to a line segment, forming leapfrog:

Inflating still more causes the bubbles to meet at the center of the original faces. This is dual. (In the drawing, the dashed arrows indicate that the meeting of three of the bubbles takes place at the singular point on the rear of the sphere.)
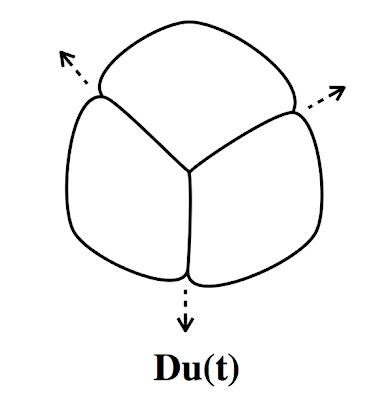
We have shown that the dual of the triangle on the sphere is the theta graph on the sphere, a graph with 2 vertices and 3 edges.
We may choose to now consider Du(t) to be the base map. Inflating its two vertices to form its truncate, we discover that we are just running the same film in reverse. We have just discovered the identity:
Tr(Du()) = Le().
Playing the rest of the film back we also discover these map operation identities:
Me(Du()) = Me(),
Le(Du()) = Tr(),
Du(Du()) = Id(),
where Id() is the identity operation, the operation that does not change the base map.
Altogether, there are 5 map operations (Id, Tr, Me, Le, and Du) that can be understood as inflations of the original vertices. This chart summarizes the sequence. The middle column shows polar views of the action of the operation on the map of a monogon on the sphere. The right column shows the action of the map operation on the quadrilateral associated with each edge of the base map. Look first at the diagrams for Id, the identity operation, to get oriented.
The map operation subdivide, Su(), inserts a new vertex at the midpoint of each edge in the base map. So Su(t) is:
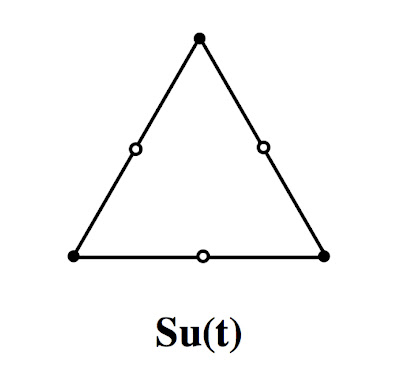
Starting from Su(t), we now have two classes of vertices, old and new, that we can inflate differently. If we choose not to inflate the new vertices, we get a rather uninteresting sequence that reprises Id-Tr-Me-Le-Du with an additional vertex in all but Me (where it is redundant.)
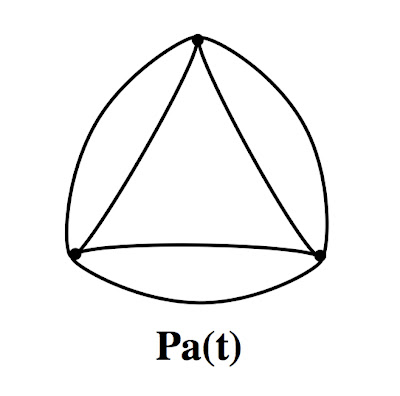
Inflating only the new vertices first gives a truncation of only the new vertices that we will call lens, Ln():

Inflating the new vertices further causes them to meet at the old vertices, which gives parallel:
Inflating still further gives chamfer:

Inflating still more closes up the non-inflated faces completely, giving radial:

The following chart summarizes the map operations produced by inflating the new, mid-edge vertices:

Finally, if both original vertices and mid-edge vertices are inflated (neither being allowed to contract to a point) we get these map operations:





