Ramification at {0, ±√3}

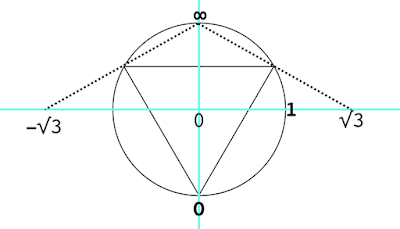
For some purposes it is preferable to have ramification points that are equally spaced in the geographic metric, for example, ramification points located at {0, ±√3} (see diagram above) rather than at {0, 1, ∞}. These will not be Belyi functions, but will have analogous uses. For example, if the three points of ramification are equally spaced around the real-number great circle, their colors can be permuted without the geographic distortion found in four of the vertex-color permuting Belyi functions.

Therefore, it may be desirable to find the unique Mobius transformation, S, that maps {0, 1, ∞}, respectively, to {-√3, 0, √3}; and its inverse, S^-1, as well. It is easier to start with the inverse since it is a mapping to {0, 1, ∞} like we saw in the previous post, in this case:

z₀ = -√3

z₁ = 0

z_∞ = √3

S^-1(z) = ((z-z₀)*(z₁-z_∞))/((z-z_∞)*(z₁-z₀))

= ((z+√3)*(-√3))/((z-√3)*(√3))

= -(z+√3)/(z-√3)

= (-z-√3)/(z-√3)

So: a = -1; b = -√3; c = 1; d = -√3

From Michael P. Pitchman's web chapter on Mobius transformations:

So, S(z) = (√3*z-√3)/(z+1) = √3*(z-1)/(z+1

Domain-coloring visualization of S:

Domain-coloring visualization of S^-1:

Domain-coloring visualization of their composition (Identity):

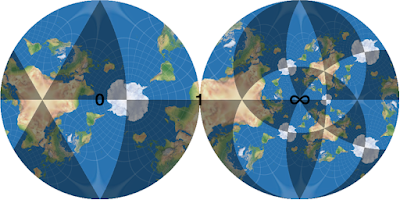
Domain-coloring visualization of S∘Tetrahedron∘S^-1:

In the above view of a tetrahedron, the North Pacific now represents vertices, Antarctica now represents mid-edges, and the Sahara represents face centers. It's easy to see that there are four faces (Sahara's) and six edges (Antarctica's), but the four vertices (North Pacifics) are harder to see.

Mobius maps to {0, 1, ∞}

Belyi functions are unique up to Mobius transformations, which are conformal maps from the Riemann sphere to the Riemann sphere that preserve, not merely infinitesimal circles, but all circles. The fate of any three distinct points determines a Mobius function. A particularly simple case is when we know which three points will map to 0, 1, and ∞. Namely, we seek a Mobius transformation S, such that:

S(z₀) = 0

S(z₁) = 1

S(z_∞) = ∞

Then S = ((z-z₀)*(z₁-z_∞))/((z-z_∞)*(z₁-z₀)).

For example, the vertex-color permuting Belyi functions can be derived this way.

Belyi functions that permute vertex colors

The canonical triangulation of a dessin has vertices of three colors: black for original vertices, white for edge centers, 'star' for face centers. The simplest Belyi functions that permute these colors in the 6 possible ways are the 6 transformations Coxeter, in Regular Polytopes, gave as an example of the operation of the symmetric group on three elements:

Here's what they look like in geographic domain coloring (geographic conventions same as previous post.) All these functions describe a half-edge or brin in different positions/orientations: its black vertex is in each case coincident with Antarctica, its white vertex coincident with Null Island.

Identity, z:

Dual, 1/z:

1-z:

z/(z-1):

1/(1-z):

(z-1)/z:

Geographic Domain Coloring & Belyi functions

Domain coloring is a popular way to visualize functions that map the complex plane to the complex plane (equivalently, the Riemann sphere to the Riemann sphere). The range space (the plane or sphere the function maps to) is given a patterned coloring and those colors are mapped back to the domain space (the plane or sphere the function maps from) by evaluating the function at every pixel in the domain. This of course involves evaluating the function a million times or so, but computers make it easy.

For the image above, the function (-64*((1/z)^3+1)^3/(((1/z)^3-8)^3*(1/z)^3)), a Belyi function for the tetrahedron, is interpreted as a Riemann-sphere to Riemann-sphere mapping. The range Riemann sphere was decorated with a map of the globe oriented in a particular way: South Pole at 0, North Pole at ∞ (on the Riemann sphere, ∞ is the point antipodal to 0,) and Null Island (shorthand for the point off the coast of Africa at 0° latitude, 0° longitude) is at 1 (on the Riemann sphere, 1 is halfway around from 0 to ∞.) The picture below shows the range sphere in the same projection used above.

Imagine the two polar projections to be hinged at 1, then imagine closing them together like a face-down book to form a two-disk map of the world.

Always keep in mind that domain coloring produces a view of the domain. In other words, the Belyi function begins with the hollow, non-physical, decorated sphere in the top picture, and stretches and folds it, in perfect registration, to cover the globe in the bottom picture. Pretty remarkable!

The dessin, in this case a tetrahedron, is found by tracing in the domain (top picture) all the pre-images of the line segment [0,1] in the range (bottom picture). This geographic domain coloring makes: vertices correspond to Antarctica's, faces correspond to Arctic Oceans, and edges to Antarctica-to-Antarctica sea voyages that pass between two copies of Africa.