Knit Anything

M. Gopi and David Eppstein have presented an algorithm that edits a surface triangulation until it admits being cut up into one long strip of triangles. The use of this algorithm has been in computer graphics. It turns out that a strip of triangles is one of the most efficient ways to describe a surface for display. It is also just what is needed to construct a fabric of any shape while working in a continuous, systematic order.

In order to go from a list of triangles to a fabric that assembles the triangles in the intended way, the knitter needs to be able to make triangles in all the possible contexts they are found in the work.

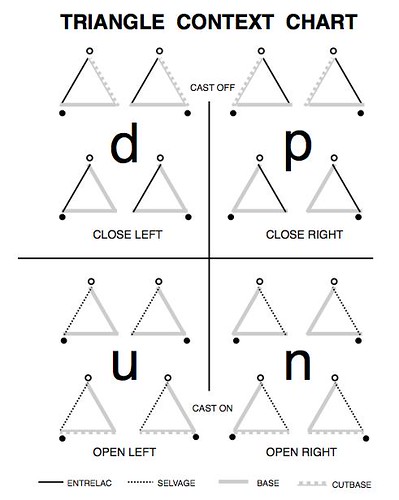
I have come up with the Triangle Context Chart as an aid to the knitter in recognizing and dealing with this small set of triangle contexts. There are in fact sixteen triangle contexts, resulting from four binary possibilities: 

1. The triangle is either an interior triangle or an exterior triangle (the only exterior triangles are the first, the cast-on triangle, and the last, the cast-off triangle.)
   
2. The yarn enters either from left or right of the triangle base.
   
3. The exterior edge of the triangle (i.e., the edge that is not interior to the triangle strip) is either a temporary selvage (open) or it is an entrelac (close), meaning it picks up stitches from the selvage of a previously knit triangle.
   
4. The exterior edge is on the left or the right.
   

Since it is obvious that the first triangle in an instruction must be the cast-on triangle, and the last is cast off triangle, the first binary possibility does not need to be explicitly stated.

Also, which side the yarn enters on is an inevitable consequence of the knitting in the preceding triangle, and the independent choice at the very start of the knitting is not usually important, so the second binary possibility can go unreported as well.

That leaves four possible contexts needing to be reported for every triangle in the knitting: open left, open right, close left, close right.  

A convenient way to write down a sequence of these four triangle contexts is with this emoticon code:

u , n , d , p .

Hint: look at the letters like smileys, but inclining your head toward the right.

I call this the undip code (accent on the first syllable of 'undip'.)

In undip, a word for the tetrahedron is:

u n d p ,

or synonymously,

n u p d .

Reference:

Gopi, M., Eppstein, D., "Single-Strip Triangulation of Manifolds of Arbitrary Topology." Proc. 25th Eurographics 2004.