Viable Adjacent Letter Mutations

There are some two-adjacent-letter edits (substitutions, insertions, and deletions) that can always be made in an undip word and the result will be another undip word. These special edits, viable adjacent letter mutations, or val mutations, intrinsically satisfy the undip grammar rules, the larger context of the two original adjacent letters need not be consulted. The term "viable," borrowed from biology, here means that the character string that results from a val mutation will indeed be a word in the undip language (and it will therefore weave unambiguously to a specific basket shape phenotype.)

In the tables below, all of the val mutations are summarized in truth table format. The first of the original adjacent letters labels the row, the second the column. The letters that will replace the two original letters are entries in the table, with e symbolizing deletion of both letters, and a blank entry indicating that no val mutation of that type (substitution, insertion, or deletion) can be made for those two letters.

Some other two-adjacent-letter edits may be viable in certain special contexts, for example insertion of the reversed spikes du and pn , but in the worst case, full context information would be needed to determine if the insertions are viable. In this sense, what are termed here val mutations are context-free.

Gene-Splicing Baskets

Starting with undp, an undip word for tetrahedrane, 

concatenate ud, an undip word for acetylene... 

...and get undpud, or benzvalene.

Insertion of undip words works just as well as concatenation. At any place in an undip word, insert another undip word and the result is a new undip word describing a hybrid shape. The new shape is 2-edge connected where the two original shapes are tenuously joined.

The structural weakness of this 2-edge join can later be healed by viable adjacent-letter (val) mutations. Val mutations are substitutions, insertions, or deletions of two adjacent letters that can be made without reference to context because they intrinsically satisfy the undip grammar rules.

Twongs Thronged at NY Maker Faire!

Visitors thronging the Twongs Table at the New York Maker Faire, September 25-26, 2010.

That's me in orange. Some tried making the carbon chemistry models (annulenes) displayed in steel, but most went freeform.

All ages advanced to level 101: having fun.

The steel models wore their undip codes attached.

Tetrahedrane in foreground, acetylene in back.

Catalan Numbers and Baskets

How many undip words are there?

The famous Catalan numbers turn up in many places ( see "Exercises on Catalan and Related Numbers" and "Catalan Addendum" by Richard P. Stanley.) One of the classic examples is counting the number of ways 2n people seated around a table can simultaneously form n handshakes without crossings. The answer to this problem is the nth Catalan number. For example, the Catalan numbers for n = {0, 1, 2, 3, 4, 5} are {1, 1, 2, 5, 14, 42}.

Another set counted by the Catalan numbers are the number of words in the Dyck language that contain n pairs of parentheses. The Dyck language comprises all strings of open and close parentheses that follow the usual rules of arithmetic expressions. For example:

()

(()) ()()

((())) ()(())) (())() (()()) ()()()

etc.

The undip language is a shuffle of two Dyck languages: a {u,d} language and an {n,p} language. We can think of {u,d} as {(,)} and {n,p} as {[,]}, but unlike a Dyck language on two types of parentheses, in a shuffle of two Dyck languages the two types of parentheses ignore each other grammatically speaking. For example, a word such as:

( [ ) ]

is permitted.

R. Cori, S. Dulucq, and G. Viennot explain how the Catalan numbers are related to the planar hamiltonian cubic maps (the structures described by undip codes) in "Shuffle of Parenthesis Systems and Baxter Permutations," Journal of Combinatorial Theory, Series A 43, 1-22 (1986):

"...hamiltonian cubic maps are planar maps with a hamiltonian circuit in which all vertices have degree three. In such a map any vertex is incident with only one edge not in the hamiltonian polygon, this edge may be inside the polygon or outside. Thus to build a 'Hamiltonian rooted cubic map' one has to choose 2k vertices among the 2n (those incident with inside edges) then draw a planar map inside the polygon (it is easy to see that this can be done in Ck ways*) and a planar map outside."

*This is easy to see because it is essentially the handshaking problem.

A map is rooted by distinguishing a vertex and direction. In a hamiltonian circuit this is combinatorially equivalent to labeling all the vertices, since, given a direction and a place to start, we can reliably label the vertices with sequential integers. Working with a rooted map, every rotation of a pattern counts as a distinct pattern because the root occupies a different place in each rotation. Counting rooted maps exhaustively counts all of the possible undip codes even when they trivially encode the same shape by virtue of merely starting at a different location on the hamiltonian cycle.

Cori, Dulucq, and Viennot go on to show that the number of rooted hamiltonian planar cubic maps are counted by the product of two sequential Catalan numbers. For a hamiltonian circuit with 2n vertices the number of maps is the product of the nth Catalan number and the (n+1)th Catalan number.

Tthe number of undip words of length 2n for n= {1, 2, 3, 4, 5} are {2, 10, 70, 588, 5544}. This is sequence A005568 in the On-Line Encyclopedia of Integer Sequences (OEIS).

For better or worse, there are a great many more undip words than there are shapes to be described by them. Synonyms will abound.

O-Knitting

Making an o-knitting vertex, Step 1: Hold Needle upright.

Toss Quoit on Needle.

Feed Thread through Needle.

Pull Quoit through Thread.

Voila! a completed vertex.

Close-up of completed o-knitting vertex.

All sorts of things that I'll call o's are available to the craftsperson: rubber bands, ponytail holders, potholder loops, etc. O's can also be made at home by slicing across a can or plastic bottle, or anything else of tubular cross-section. O's can be knit together to form 3D shapes without the increases and decreases traditionally depended upon in knitting and crochet. O-knitting can optionally be guided by a string of letters drawn from a four-letter alphabet, what I call an undip word, that describes the step-by-step construction of a surface. Using undip words, o-knitting becomes a sort of genetic knitting.

There are only two big things to learn about o-knitting: how to make a vertex, and how to follow an undip code. Learn those two things and you will be a able to build a spaceship on a desert island, or at least a floppy grass model of one.

An o-knitting vertex is an inter-looped union of three o's. An o-knitting vertex is a reciprocal structure. That is, each of the o's plays the same role in the union. We'll give each o a name according to how it first enters the union, but by the time we are done making the vertex they'll all be equivalent. An o-knitting vertex is a three-way version of Mrs. Bright's (four-way) True Lovers' Knot (Ashley Book of Knots #2425.)

OK, let's make an o-knitting vertex. The first o is called Needle. Except at the very first vertex (call it the origin,) Needle will already be attached to the work. Hold Needle with its free end upward.

The second o is called Quoit. Quoit is always free at both ends. Toss Quoit over Needle.

The third o is called Thread. Feed Thread through Needle. It is best to always feed Thread from the right side (or always from the left side, if you prefer.) Feeding from the same side makes vertices that are all of the same handedness, giving the fabric a more even look. Thread will be free at both ends when making u and n vertices, but already in the work when making p and d vertices.

Now feed Quoit through Thread (i.e., through the end of Thread that pushed out through Needle.)

Voila! One vertex made. 3D shapes are made by repeating the above moves.

3-D shapes may be specified by an undip word or genotype, a character string made up of the four emoticons: u, n, d, and p.

For example, a genotype for the cube is

nuupdd .

The the letters are called emoticons because they are meant to be read with the head tilting sideways (toward the right) and their meanings are visually obvious—no need to wake up the left side of the brain at all. The four o-knitting actions they encode are:

"Open left," meaning: "make a new vertex and leave the o on the left side dangling," (i.e., continue to the right. )

"Open right," meaning: "make a new vertex and leave the o on the right side dangling," (i.e., continue to the left.)

"Close left," meaning: "make a new vertex employing the nearest dangling o on the left side."

"Close right," meaning: "make a new vertex employing the nearest dangling o on the right side."

(Figure out for yourself which emoticon encodes which action.)

Note that at a close vertex the roles of Needle and Thread can be assigned so that Thread enters Needle consistently from the right (or, alternatively, consistently from the left.) A switch causes no confusion about how to continue, since just a single o is left dangling after a close vertex.

You have to work consistently from the outside of the piece (or consistently from the inside.) Early on this will mean taking care that o's do not get twisted. At the end, should you find you have made the enantiomorph of what you intended—no problem. Just evert the piece through one of its openings.

Quoit must always be free at both ends, but at the final vertex all three o's will already be attached to the work. The final vertex must be joined by some other technique. The simplest way is to add a fourth o as Quoit, making the last vertex a regular fourway Mrs. Bright's knot. The extra o is left dangling, permanently marking the origin (and terminus) of the undip word.

Hansel & Gretel's Hint: mark your very first o with a twist tie or special color—should you get lost, you can can retrace the word from the beginning.

Embedded graphs come in families of four

Cubic graph (the dual)

Triangulation (the primal)

Radial graph

Medial graph

Kagome weave

Anyam Gila

In unit weaving we are constantly dealing with families of four closely related graphs: a triangulation (the primal graph), a cubic graph (the dual graph), a medial graph, and a radial graph. Kagome (triaxial weaving) is closely related to the medial graph of a triangulation. Anyam Gila (or "mad weave"), a triple-layered version of kagome, has an outward appearance that suggests the radial graph of a triangulation.

Some facts from the Handbook of Graph Theory:

1. An embedded graph M is a medial graph of some graph G if and only if M is 4-regular and the faces can be properly 2-colored.

2. An embedded graph R is a radial graph of some graph G if and only if R is bipartite and every face is a quadrilateral.

3. The medial graph M of an embedded graph G is identical to the medial graph of the dual G*. The radial graph R of G is identical to the radial graph of the dual G*. The embedded graph and its dual are the only two graphs whose medial and radial graphs are M and R respectively.

Any surface-embedded graph can play the role of "primal," and it is guaranteed to have a dual, medial, and radial, all of which are discoverable through simple constructions called map operations. It is a convenience of speech that we identify one graph as the primal and the other as the dual: the roles could just as easily be reversed with no effect on the rest of the foursome. The same, however, is not true for the medial and radial (which are also mutually dual,) because radial graphs and medial graphs each have special characteristics as indicated in Facts 1 and 2 above. Thus, most graphs belong to only one foursome: the one formed when they are the primal (or equivalently the dual.) The few graphs that qualify as medial (or radial) graphs belong as well to a second foursome: the one where they are the medial (or radial.)

The familiar square grid makes for a special case. It is dizzyingly at once self-dual, self-medial, and self-radial. This deep symmetry of the grid pattern helps explain why 10,000 years of biaxial weaving has not gotten us very far in understanding weaving more generally.

When plain weaving is not in some artificially arranged conformation, just two threads cross at each crossing. A graph of a plain weaving (crossings being represented by vertices and threads being represented by edges) is therefore four-regular (i.e., exactly four edges meet at each vertex.) That satisfies the first requirement in Fact 1.

The relevance of the second requirement in Fact 1 can be seen from an observation by Snelson (U.S. Patent 6,739,937), that each thread in a plain weaving is a boundary between a left-handed opening and a right-handed opening. Such an arrangement is only possible if the fabric openings can be properly 2-colored (such a coloring is popularly known as a chess-coloring or checkerboard-coloring.)

The necessary and sufficient requirements for a graph to be a medial graph are thus the same requirements necessary and sufficient for a graph to specify a plain weave: the 4-regular graph specifies the two-dimensional arrangement of threads, and the 2-coloring of its faces tells us which openings are to be left-handed or right-handed. The handedness of the openings, in turn, tells us how to arrange the threads at each crossing, in the third dimension, to produce a true plain weave.

In this light, Fact 1 establishes that every medial graph describes two enantiomorphic plain weaves (one for each of the two alternate left/right color assignments.)

In the same light, the converse assertion in Fact 1 (i.e.: if M is 4-regular and the faces can be properly 2-colored, then M is a medial graph) establishes that no plane weave exists that is not described by a medial graph.

In short, weaving has found the light switch after thousands of years of fumbling in the dark:

1. We now know that every compact surface can be plain-woven-- no matter the topological complexity or the orientability of the surface. (The term "compact" merely rules out some mathematically defined surfaces that cannot be realized by any technological means. In layman's terms we can plain-weave any surface.)

2. We can plain-weave that surface in essentially any pattern (we are not limited to familiar biaxial or triaxial weaves.) Any graph, any drawing of edges and vertices we choose to put on the surface, can direct the weaving via its medial graph.

3. We know constructively how to proceed in every case.

4. We know that our construction process is universal: there exist no other plain weaves but those described by medial graphs.

We have 1-3 above from the 2009 topological proof by Akleman, Chen, Xing, and Gross (see my earlier post Proving Weaving) I believe the universality result is new.

Undip codewords as lattice walks

Any undip word can be identified with a 2D lattice walk where the allowed steps are N, S, E, W, the walk begins and ends at the origin (such a lattice walk is called a loop), and the walk is furthermore confined to the first quadrant (quarter plane).

Identify 'u' with an North step, and 'd' with an South step (mnemonically 'up' and 'down'). Similarly identify 'n' with an East step and 'p' with a West step.

The "balanced parentheses" rules for undip words (where |x| denotes the number of occurences of the letter 'x') are:

|u| = |d|

|n| = |p| ,

These rules guarantee that total South steps equal total North steps, and total West steps equal total East steps; thus, if a codeword-designated walk begins at the origin, it will end at the origin.

The "nested parentheses" rules guarantee that the walk stays in the first quadrant. The rules are:

|u| >= |d|

|n| >= |p|

for any predicate of an undip word.

In other words, at no point in the spelling of an undip word will there have been more d's than u's, or more p's than n's. On the lattice this means that the walk can never go south or west of the origin-- it is confined to the NorthEast quadrant.

Undip codes and Euler's Formula

Any graph embedded in the sphere must obey Euler's formula:

F - E + V = 2 ,

where F, E, and V are the number of faces, edges, and vertices. Since every hamiltonian cubic graph embedded in the sphere has a valid undip codeword, a reasonable question is how (and whether) having a valid undip codeword can guarantee compliance with Euler's Formula.

Euler's formula is a bit simpler for cubic graphs. Cutting a cubic graph at every mid-edge, leaves a disconnected set of vertices, each still holding on to three half-edges. Thus,

E/V = 3/2 .

That fixed E/V ratio reduces Euler's formula for a cubic graph to

F - V/2 = 2 ,

or

F = V/2 + 2 .

In a valid the undip codeword there is one letter for each vertex. For every open letter, 'u' and 'n,' there is a matching close letter, 'd' and 'p'. Therefore a count of the occurrences of d and p, |d, p|, will count one half of the vertices:

|d,p| = V/2 .

Euler's formula then becomes

F = |d,p| + 2 .

It is easy to see that in weaving a valid undip codeword this rule is always obeyed. Each close letter, 'd' or 'p', completes a face, until we come to the final close letter. The final close letter also completes the hamilton cycle and thereby closes an additional face on both the left and the right-- that provides the final "+ 2" faces.

What can undip codewords code?

Twongs and twogs can make more shapes than the four-letter undip code can code.

A graph must have a Hamilton circuit in order to be undip encoded. (Note that Hamiltonicity is a property of the graph, not the embedding.) That leaves out cubic graphs with self-loops (cubic pseudographs proper) since they can never be Hamiltonian. Only cubic multigraphs can be undip coded.

Furthermore, the embedding must be in the plane (or equivalently the sphere) in order for the coded side bonds to link up predictably. On a higher genus surface, the whole surface area might be encoded in the predictable planar way, but there will remain a closed curve (i.e., the polygon of the plane model, see A Combinatorial Introduction to Topology by Michael Henle) that cannot be seamed across without encountering a surprise.

The photo above shows a digonal prism. Even though a digonal prism is a graph embedded in the sphere, it is not considered a polyhedron by most definitions. For one thing, it contains two-sided faces (digons); for another, it is only 2-edge connected. (Cutting just the two edges shown vertical in the photo would separate the graph into two components.) Note that these are properties of the graph itself, not the embedding. Graphs that are only 1-edge or 2-edge connected make weak structures but they certainly are of sculptural interest. Polyhedron or not, 'udud' codes the digonal prism nicely.

Taking the adjective "plane" to mean "embedded in the plane or sphere," the undip code can encode Hamiltonian plane cubic multigraphs.

What can twongs make?

Twongs and twogs can make 3D embeddings of cubic pseudographs.

A graph is called cubic if three edges meet at each vertex. Simple graphs permit only a single edge to link two distinct vertices, multigraphs allow more than one edge to link two distinct vertices, pseudographs also allow a vertex to link to itself (i.e., form a self-loop.) A graph is an abstraction: a set of symmetrical relations (edges) between pairs of members of a set (the set of vertices). For example, the friendships (edges) between persons (vertices) listed in a phonebook. Such an abstraction has no geometry until we make some decisions not specified in the graph itself in order to place (embed) its vertices and edges in 3D space, or on the Euclidean plane, or on some other surface or in some other space. Sometimes a given graph can be embedded in a space in fundamentally different ways, e.g., a left-handed and a right-handed version. The embedding, not the graph itself, is our guide to these important practical details. See Topics in Trivalent Graphs by Marijke van Gans for a clear mathematical exposition.

If twongs and twogs are made long enough, they can be used to realize any 3D embedding of a cubic pseudograph. The construction above is an embedding of the smallest cubic pseudograph having loops. I call it loop-loop. An embedding of the smallest cubic pseudograph without loops (thus also a multigraph) is shown below. I call this one bang-bang.

twongs

These are what I call twongs.

A twong is a helical length of wire that has been bent in four places. Twongs are made by twisting up a pair of wires (these particular ones have been twisted to a helical wavelength of about 5 wire diameters), unravelling them, cutting them to length (these have been cut to a length of 12 helical wavelengths), and then bending. I have been working by hand, so I have been limited to 9 gauge (0.14 inch diameter) steel wire and smaller. Wire is made over a vast range of diameters, so twongs can be almost any size.

The main thing about twongs is that they twine together, three at a time, to form vertices. I've made a video about twining them together. With enough twongs you can make any shape having exclusively 3-valent vertices (three edges meeting at a vertex.) The tetrahedron, cube and dodecahedron are famous 3-valent (i.e., cubic) polyhedra, but there are many more. For example, there are 14,501 isomers of the dodecahedron, that is, different shapes but all with the same number of faces, vertices, and edges as the dodecahedron, and they are likewise all 3-valent. The C-60 buckyball is also all trivalent. Its isomers are effectively uncountable, being in excess of 10 to the 22nd. Yikes!

The are so many cubic polyhedra that, given enough vertices, we can use one to approximate any simple closed (i.e. genus zero) surface. The approximation is never smooth because all lengths are the same, nonetheless, there are many cases where a crinkly surface is a good enough, or where a crinkly surface can be made smooth by some mechanical process. In any case, the alternative--custom cutting every piece (I've tried it)--is a royal headache, and no custom-cut part is ever re-useable.

An astonishing thing about genus zero cubic graphs (let's just toss out the very small number that are non-Hamiltonian) is that they can be identified with words in a language having a very simple grammar. Formally the language is known as the shuffled Dyke language on two types of parentheses. Instead of parentheses we will want to use the following letters:

u, n, d, p

corresponding to (look at them tilting your head to the right) the following twiner's actions

"open left", "open right", "close left", and "close right"

The moves are as follows:

To start, pick up a very first twong and mark it with a twist-tie. This is insurance against getting lost--you can always retrace from the beginning if you know where that is. It also symbolizes that the very first twong is the work in progress. At any later vertex, at least one twong will be already part of the work in progress.

The first letter is always an "open" action, i.e., 'u' or 'n'. In an "open" action you just build a vertex--that's the same for "open left" or "open right." The difference comes when you exit the newly built vertex. To leave a twong "open (on the) left", we must build onto the right twong, Likewise to leave a twong "open (on the) right" we must build onto the left twong. That's all there is to 'u' and 'n,' they just tell us which way to go next.

Close actions require us to incorporate a previously placed twong into the current vertex. According to the letter, we are to look either to the left or the right for this previously placed twong. If there is more than one available on that side we simply choose the nearest one on that side (i.e., most recently placed). This is the same way nested parentheses close, hence the connection to parenthesis languages. Departing a close action is simple since only one of the three twongs will still have a free end.

The last vertex is always a close action. Implicitly, the first twong (the one marked by the twist tie) must be incorporated in this vertex along with the twong indicated by the final letter.

I have more about these "undip" codes in this year's Proceedings of the ISAMA.

Knit Anything

M. Gopi and David Eppstein have presented an algorithm that edits a surface triangulation until it admits being cut up into one long strip of triangles. The use of this algorithm has been in computer graphics. It turns out that a strip of triangles is one of the most efficient ways to describe a surface for display. It is also just what is needed to construct a fabric of any shape while working in a continuous, systematic order.

In order to go from a list of triangles to a fabric that assembles the triangles in the intended way, the knitter needs to be able to make triangles in all the possible contexts they are found in the work.

I have come up with the Triangle Context Chart as an aid to the knitter in recognizing and dealing with this small set of triangle contexts. There are in fact sixteen triangle contexts, resulting from four binary possibilities: 

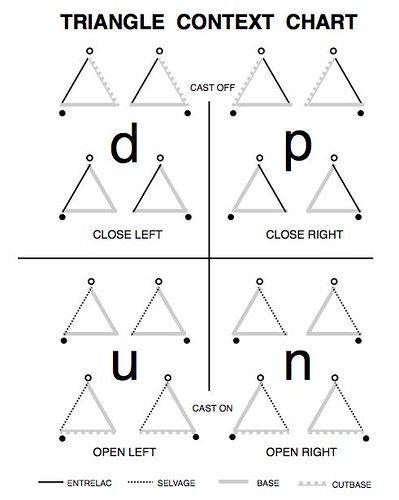
1. The triangle is either an interior triangle or an exterior triangle (the only exterior triangles are the first, the cast-on triangle, and the last, the cast-off triangle.)
   
2. The yarn enters either from left or right of the triangle base.
   
3. The exterior edge of the triangle (i.e., the edge that is not interior to the triangle strip) is either a temporary selvage (open) or it is an entrelac (close), meaning it picks up stitches from the selvage of a previously knit triangle.
   
4. The exterior edge is on the left or the right.
   

Since it is obvious that the first triangle in an instruction must be the cast-on triangle, and the last is cast off triangle, the first binary possibility does not need to be explicitly stated.

Also, which side the yarn enters on is an inevitable consequence of the knitting in the preceding triangle, and the independent choice at the very start of the knitting is not usually important, so the second binary possibility can go unreported as well.

That leaves four possible contexts needing to be reported for every triangle in the knitting: open left, open right, close left, close right.  

A convenient way to write down a sequence of these four triangle contexts is with this emoticon code:

u , n , d , p .

Hint: look at the letters like smileys, but inclining your head toward the right.

I call this the undip code (accent on the first syllable of 'undip'.)

In undip, a word for the tetrahedron is:

u n d p ,

or synonymously,

n u p d .

Reference:

Gopi, M., Eppstein, D., "Single-Strip Triangulation of Manifolds of Arbitrary Topology." Proc. 25th Eurographics 2004.

Proving Weaving

The Plain-Weaving Theorem

Akleman, Chen, Xing, and Gross (ACXG) have published a proof that every polygonal mesh describes a plain-weaving (a term to be precisely defined below.) If so inclined, we may count two plain-weavings by considering weavings differing only in textile handedness (indicated by the helical pattern of threads around a specified opening in the fabric) to be distinct.

(Note that any weaving can theoretically be everted—turned inside-out—through an opening. While this does not alter the textile handedness of the work, it does change the handedness of the work as a whole. For example, eversion turns a right hand glove into a left hand glove. So it may fairly be said that the everted version does not weave the same surface. Nonetheless, the same set of weavers, woven in the same handedness, may weave either surface. The basket maker will need a hint to resolve this ambiguity.)

ACXG's result is fundamental. Their proof is fully three-dimensional and topological, so there can be no objections as to its physical reality. The proof leaves no escape for a compact surface of any sort -- all compact surfaces, be they orientable or non-orientable, high-genus or low, are doomed to be woven as baskets. The escapees are the non-compact surfaces, i.e., surfaces of infinite extent, or infinite topological genus, or having excluded interior points or open boundaries—but such are not buildable by any method.

And there is also no escape for any particular kind of mesh. Their result, which I will take to calling the Plain-Weaving Theorem (PWT,) states that all polygonal surface meshes describe a way to weave the surface. There is great difficulty imagining any way to subdivide a surface into local neighborhoods that is not in effect a polygonal surface mesh. Admit it or not, computer scientists are doomed to be virtual basket weavers for the rest of history.

Having this 3D theorem in hand, I want to turn to a purely 2D representation of plain weaving which is easy to visualize, easy to characterize as a mathematical object, and probably sufficient for all artisanal purposes.

The Definition of Plain-Weaving

I adopt ACXG's definition of plain-weaving—which differs from common usage in the textile field. In their definition, a plain-weaving "consists of threads that are interlaced so that a traversal of each thread alternately goes over and under the other threads (or itself) as it crosses them." This definition takes in some weaves such as the kagome (also known as open hexagonal or triaxial) weave that are not considered "plain" in the textile field, but the PWT rewards us with the insight that all plain-weaves newly defined are really the same thing and can be intermixed freely.

Weaving and Chess-Colorings

Kenneth Snelson, in the specification of his patent on 3D weaving, U.S. Patent 6,739,937, makes a significant observation: we can treat weaving as a 2D arrangement of openings rather than a 3D arrangement of threads. To turn the old saw around, Snelson is saying we should watch the hole, not the donut.

As Snelson observes, the openings in a plain-weave fabric have a handedness that can be compared with the handedness of a screw-thread. In going from over-one-thread to under-the-next whilst going around an opening, the threads have a ramp-like geometry. If we arbitrarily choose a direction of travel around the periphery of the opening, and identify that direction with the direction of the curled fingers, then using the ramps in this direction converts the advancing movement into a motion in a perpendicular direction. We can identify this perpendicular direction with the direction of the thumb extended. Uniquely only a left or a right hand is capable of carrying both of these identifications. We can therefore unambiguously label every opening in a weave as right or left, R or L, or perhaps color code them black or white. Since no reference has been made to a side of the fabric, the handedness of the openings is intrinsic to the weaving: it matters not which side we view or whether the work is everted or not.

Also, there can be no question that the threads in a plain-weave agree on the handedness of any opening they share—otherwise they would not be able to reach a mutual arrangement about whose turn it is to go over or under where they cross. Like a circle of fallen dominoes, they must all lean one way.

Snelson observes that adjacent openings (i.e., openings on opposite sides of the same thread) have opposite handedness. This follows almost anatomically: if two hands have curled fingers pointing in the same direction, and extended thumbs pointing in the same direction, they surely must be a right and a left.

A coloring of the faces of a map with two colors, say black and white, such that adjacent faces have different colors is called a chess-coloring (I prefer this shorter term over "checkerboard coloring") Not all maps can be chess-colored, but a map operation, medialization, is known which converts any map into a chess-colorable map (Deza and Dutour.) The resulting map is called the medial of the original map (itself called the primal), and the result of medialization is the same whether we start from the primal map or its dual. In map operation notation (see Diudea et al. for an explanation of the notation):

Me(M) = Me(Du(M))

This is the result reported in ACXG that a mesh and its dual describe the same weaving. As Deza and Dutour have pointed out, medialization can be applied to any map (surface-embedded graph) to produce a chess-colorable map, hence every surface-embedded graph has a plain-weaving discoverable through this map operation.

In knot theory terms, a plain weaving is an alternating link. The medial graph is the projection (or more properly the shadow when crossing information is omitted) of an alternating link. The chess-coloring of the medial graph corresponds the checkerboard-coloring of the link projection, and the primal and dual maps above are the two Tait graphs of the link projection (see explanation of terms in Dasbach and Lowrance.) Because the link is alternating it is described in full by its chess-coloring.

Mathematically the study of plain-woven baskets reduces to the study of chess-colorings on surfaces, and such a chess-coloring contains essentially all the information the weaver needs to weave the basket.

References:

Akleman, E., Chen, J., Xing, Q., and Gross, J. L. 2009. Cyclic plain-weaving on polygonal mesh surfaces with graph rotation systems. ACM Trans. Graph. 28, 3 (Jul. 2009), 1-8. DOI= http://doi.acm.org/10.1145/1531326.1531384

Snelson, K., U.S. Patent 6739937, Space Frame Structure Made by 3D Weaving of Rod Members.

Deza, M., and Dutour, M., Zigzags and central circuits for 3- or 4-valent plane graphs, http://www.liga.ens.fr/~deza/Sem-ZigCc/ZigCcConf.pdf

Diudea, M., et al., 2003, Leapfrog and Related Operations on Toroidal Fullerenes, Croatia Chemica Acta, 76 (2) 153-159, http://pubwww.carnet.hr/ccacaa/CCA-PDF/cca2003/v76-n2/CCA_76_2003_153-159_diudea.pdf

Dasbach, O. and Lowrance, A. 2010. Turaev Genus, Knot Signature, and the Knot Homology Concordance Invariants, http://arxiv.org/pdf/1002.0898